
Escribir las longitudes de dos lados y un 0 en el lado a calcular. Pulsar el botón Calcular para ver el resultado (se muestra en el cuadro donde está el 0).
Los resultados se muestran aproximados con 2 decimales.
| Lados | Otros datos |
|
a = |
Área: |
|
b = |
Perímetro: |
|
h = |
α ≅ º |
|
β ≅ º |
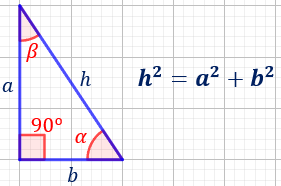
El teorema de Pitágoras establece la relación existente entre los 3 lados de un triángulo rectángulo. Esto nos permite calcular la longitud de cualquiera de los lados a partir de la longitud de los otros dos.
La fórmula del teorema de Pitágoras es
siendo
Operando en la fórmula podemos obtener fórmulas para calcular los catetos:
A continuación, proporcionamos 5 ejemplos o problemas de aplicación del teorema de Pitágoras resueltos paso a paso.

¿Cuánto mide la hipotenusa de un triángulo rectángulo si sus catetos miden 3 y 4 metros?
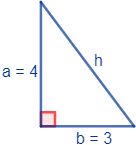
Los datos del triángulo son:
Por el teorema de Pitágoras podemos calcular la hipotenusa:
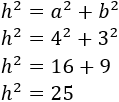
Como la hipotenusa está al cuadrado, se calcula la raíz cuadrada:

La hipotenusa mide 5 m.

Calcular el área (sin aproximar) de un triángulo rectángulo sabiendo que su hipotenusa mide \(\sqrt{5}\) cm y su altura mide \(\sqrt{3}\) cm:
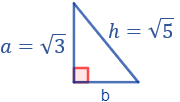
Los datos del triángulo son:
El área de un triángulo es base por altura dividido entre 2. La altura es a = \(\sqrt{3}\), pero no conocemos la base del triángulo, b. Aplicamos Pitágoras para calcularla:
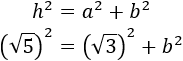
La raíz cuadrada desaparece al elevarla al cuadrado:

Como ya tenemos la base, podemos calcular el área del triángulo rectángulo:

El resultado de multiplicar dos raíces cuadradas es igual a la raíz cuadrada del producto de sus radicandos:
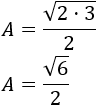
Luego el área es, aproximadamente, 1,22 cm.

Se quiere colocar un cable que parte desde la cima de la torre Eiffel (300 metros de altura) y que termina en el suelo a 150 metros del centro de la base de la torre:
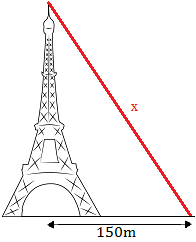
Calcular la longitud que debe tener el cable.
Los datos del triángulo son:
La altura y la base del triángulo rectángulo son 300 y 150 metros, respectivamente. La longitud de cable es la hipotenusa y se puede calcular aplicando el teorema de Pitágoras:
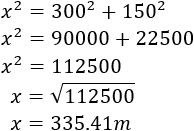
El cable debe medir aproximadamente 335.41 metros.

El área de un triángulo rectángulo mide \(A = 15\) cm2 y su base mide \(b = 6\) cm:

Calcular cuánto mide la hipotenusa, \(h\).
El área de un triángulo es base (\(b\)) por altura (\(a\)) divido entre 2:
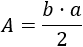
Como sabemos que el área es \(15\) cm2 y que la base es \(b = 6\) cm, podemos calcular la altura:
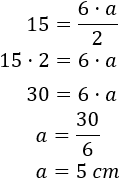
La altura del triángulo es 5 cm.
Luego los datos del triángulo son:
Finalmente, calculamos la hipotenusa aplicando Pitágoras:
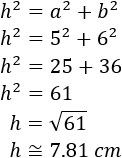
La hipotenusa mide, aproximadamente, 7.81 cm.
La base del siguiente triángulo no rectángulo mide 50 cm, su altura es \(a = 30\) cm y su lado \(h= 36,06\) cm:

Calcular cuánto mide el lado \(x\).
La altura divide al triángulo en dos triángulos rectángulos:
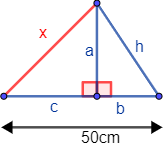
Nos fijamos en el triángulo rectángulo de la derecho. Sus datos son:
Aplicando el teorema de Pitágoras se obtiene la longitud del lado \(b\):
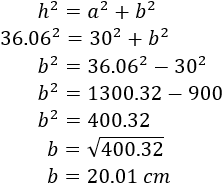
La suma de la base de los dos triángulos rectángulos es igual a 50 cm, luego tenemos
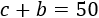
Al conocer \(b\), se puede calcular el lado \(c\):
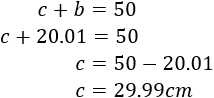
Del triángulo de la izquierda se conocen la base (\(c\)) y la altura (\(a\)), así que se puede calcular su hipotenusa (\(x\)) aplicando Pitágoras:
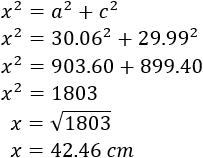
Por tanto, el lado x del triángulo no rectángulo mide, aproximadamente, 42,46 cm.
Fuentes:
Otras calculadoras:
Teorema de Pitágoras online © - 2018